A section of rope hangs freely from your hands. What’s the shape? People had thought for some time that it might be parabola. It turns out it has the so-called catenary shape. A parabola is technically a linear combination of quadratic, linear and constant terms (i.e. a 2nd-degree polynomial) while a catenary is a linear combination of hyperbolic cosine and sine functions and a constant, so the two combine very different functions in nature.

But the plots are barely distinct as the image above shows with gray for an imaginary parabola. It would be the right shape in fact had the rope supported a uniform horizontal weight as in the case of bridges where the suspension cables are parabolic.

Here’s a little puzzle. Let’s say you pull down a catenary in the middle and form an inverted tent (how can you do that, but with your third limb of course). The center of gravity is now located half-way down. Let go of it and the rope goes back to catenary. What about the center of gravity: does it sink, rise or perhaps stay at the same height?
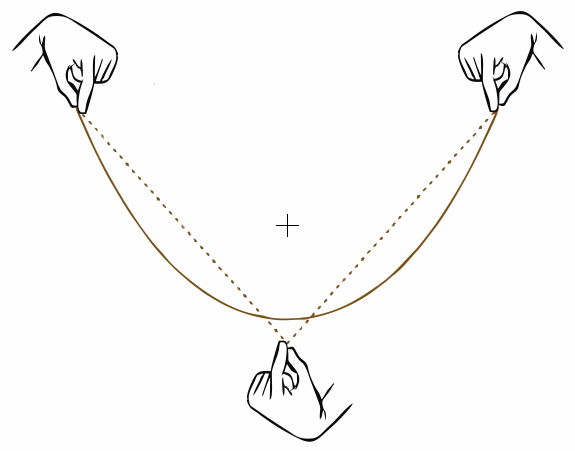
Solution: the center of gravity sinks as you let go of the V-shaped rope. The potential energy buildup that is released comes from you pulling the rope down (and rising the center of gravity).

The picture of the cats in your text is wonderful. Could I use it in my blog Rosa Soham? I feel closely related to Catenary Cat family :-) . Of course with the link to your web?
Best wishes Rosa at soham@centrum.cz